Skip to main content
Journal ArticleOPEN ACCESS

Dynamic Spin-Lattice Coupling and Nematic Fluctuations in NaFeAs

Physical Review X (2018) 8(2)
DOI: 10.1103/PhysRevX.8.021056
14Citations
Citations of this article
30Readers
Mendeley users who have this article in their library.

Abstract

We use inelastic neutron scattering to study acoustic phonons and spin excitations in single crystals of NaFeAs, a parent compound of iron-pnictide superconductors. NaFeAs exhibits a tetragonal-to-orthorhombic structural transition at Ts≈58 K and a collinear antiferromagnetic order at TN≈45 K. While longitudinal and out-of-plane transverse acoustic phonons behave as expected, the in-plane transverse acoustic phonons reveal considerable softening on cooling to Ts and then harden on approaching TN before saturating below TN. In addition, we find that spin-spin correlation lengths of low-energy magnetic excitations within the FeAs layer and along the c axis increase dramatically below Ts and show a weak anomaly across TN. These results suggest that the electronic nematic phase present in the paramagnetic tetragonal phase is closely associated with dynamic spin-lattice coupling, possibly arising from the one-phonon-two-magnon mechanism.

Figures

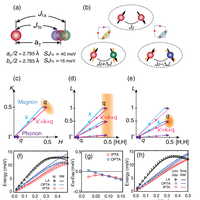
  • FIG. 1. (a) Left: Schematics of the Fe layers in NaFeAs. Red spots represent Fe atoms, and the tetragonal (orthorhombic) unit cell is shown by the green (blue) shaded square. The middle and right panels are the two orthorhombic domains. The yellow and red areas are the tetragonal unit cells with opposite shear distortions. The arrows in the middle panel indicate the spin direction in the AF ordered phase. The orthorhombic lattice parameters are ao ¼ 5.589 Å and bo ¼ 5.569 Å. (b) A particular IPTA phonon mode with a momentum propagating horizontally to the right but with Fe atoms oscillating vertically. Here, λ is the size of the probing domain, and it is inversely related to q. (c) The three different equivalent positions in reciprocal space used in our neutron scattering measurements in order to determine all three acoustic phonon branches. The purple arrows with q are the momentum of the measured phonons along the ½H; 0; 0 direction, and the double-headed arrows represent the phonon polarizations along the a (red, LA), b (blue, IPTA), and c (green, OPTA) axes. (d) The corresponding dispersions of the three phonon modes at 100 K estimated from data in Ref. [37]. The inset shows an expanded view of the low-energy part of the dispersion.
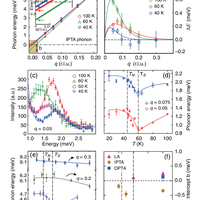
  • FIG. 2. (a) Temperature dependence of the phonon dispersions of the IPTA mode near the zone center at 100 K, 60 K, and 40 K. The inset shows the expanded view of the low-energy part of the dispersions. (b) The estimated amplitude of the softening of the IPTA phonons at difference temperatures obtained by subtracting an assumed linear dispersion E ¼ vq. The solid lines are guides to the eye. (c) Temperature dependence of constant-q scans at q ¼ 0.05 for the IPTA mode. (d,e) Temperature dependence of the phonon energy measured at q ¼ 0.05, 0.075 and 0.1,0.15, respectively. The phonon softening on cooling to Ts is observed at q ¼ 0.05, 0.075, and 0.15 r.l.u. but absent at q ¼ 0.20 and 0.3 r.l.u. The phonon hardening below Ts is seen for wave vectors below q ¼ 0.2 r.l.u. (f) Temperature dependence of the intercept b estimated for all three acoustic branches shown in Fig. 1(d).
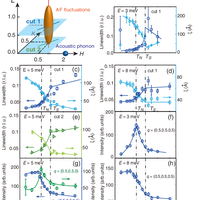
  • FIG. 3. (a) Sketch of the reciprocal space in which AF spin fluctuations and acoustic phonons are marked as a yellow ellipsoid and a blue sphere. The directions along which we measured in the experiment are shown as blue, green, and red lines. (b)–(e) Temperature-dependent linewidths and correlation lengths of the low-energy spin fluctuations. They are measured along the cut-1 direction at (b) 3 meV, (c) 5 meV, and (d) 8 meV, and (e) along the cut-2 direction at 5 meV. (f)–(h) Temperature dependence of the peak intensity in each scan. It is clear that there are negative correlations between the peak intensity and the peak width before the system enters into the AF ordered state, representing a redistribution of spectral weight in the nematic phase below Ts. The vertical dashed lines mark the magnetic and structural transition temperatures.
  • FIG. 4. (a)–(d) Constant-E (E ¼ 2 meV) scans along the cut-3 direction as shown in Fig. 3(a) at 45 K, 50 K, 55 K, and 60 K. Background scans are obtained by measuring at q ¼ ð0.4; 0.4; LÞ and ð0.6; 0.6; LÞ and are subtracted from the raw data. The scan at 60 K is featureless. On cooling to 55 K, two weak peaks show up around L ¼ 0.5 r.l.u. Upon further cooling, these peaks become prominent at T ¼ 45 K. They disappear below TN due to the opening of a spin gap. The total magnetic scattering intensity increases on cooling. The solid lines are fits with a periodic Lorentz function [37]. (e)–(g) Temperature dependence of the linewidths and correlation lengths of the low-energy spin fluctuations along the c-axis direction [cut 3 in Fig. 3(a)] at 2 meV, 3 meV, and 5 meV. (h) Temperature dependence of the integrated intensity along the cut-3 direction at different energies [37].
  • FIG. 5. (a) Schematics of the nearest-neighbor Fe‐Fe bond. The small difference between ao=2 and bo=2 and the large difference between J1a and J1b render a non-negligible ΔJ=Δr, which entangles the lattice and magnetism. (b) One pair of magnetic Fe ions in the paramagnetic tetragonal phase with the magnetic binding energy of Eb ¼ J0S1S2 cos θ. As the Fe-Fe bond stretches, the spin exchange coupling increases; thus, there is an energy transfer from the lattice to the spin system. (c) The scattering triangle required by the momentum conservation in the dynamic spin-lattice coupling process within the ½H;K plane. (d,e) The momentum triangles in the ½H;H; L plane above and below Ts. As spin fluctuations undergo a 2D-to-3D transition, a large part of the spin-lattice-coupling scattering channel would be blocked. (f) Comparison of the phonon dispersions obtained from DFT calculations with (markers, M) and without (solid lines, NM) magnetism, assuming a tetragonal lattice. We note that the nonmagnetic tetragonal phase does not really exist in NaFeAs since spin correlations are strong at temperatures far above TN and Ts. (g) Wave-vector dependence of EM − ENM for IPTA and OPTA phonon modes. (h) Comparison of the phonon dispersions obtained from DFT calculations with a nonmagnetic (NM) Fe site assuming orthorhombic (markers) and tetragonal (solid lines) lattices. The black, blue, and red colors represent LA, OPTA, and IPTA phonon modes.

References Powered by Scopus

What drives nematic order in iron-based superconductors?

Nature Physics
978Citations
N/AReaders
Get full text

Antiferromagnetic order and spin dynamics in iron-based superconductors

Reviews of Modern Physics
619Citations
N/AReaders
Get full text

Theory of electron nematic order in LaFeAsO

Physical Review B - Condensed Matter and Materials Physics
608Citations
N/AReaders
Get full text
View more at Scopus

Cited by Powered by Scopus

Quantum mechanical modeling of magnon-phonon scattering heat transport across three-dimensional ferromagnetic/nonmagnetic interfaces

Physical Review B
69Citations
N/AReaders
Get full text

Correlation-driven electronic reconstruction in FeTe<inf>1−x</inf>Se<inf>x</inf>

Communications Physics
28Citations
N/AReaders
Get full text

Local orthorhombic lattice distortions in the paramagnetic tetragonal phase of superconducting NaFe<inf>1−x</inf>Ni<inf>x</inf>As

Nature Communications
23Citations
N/AReaders
Get full text
View more at Scopus

Register to see more suggestions

Mendeley helps you to discover research relevant for your work.

Already have an account?

Cite

CITATION STYLE

APA

Li, Y., Yamani, Z., Song, Y., Wang, W., Zhang, C., Tam, D. W., … Dai, P. (2018). Dynamic Spin-Lattice Coupling and Nematic Fluctuations in NaFeAs. Physical Review X, 8(2). https://doi.org/10.1103/PhysRevX.8.021056

Readers over time

‘18‘19‘20‘21‘22‘23‘240481216

Readers' Seniority

Tooltip

PhD / Post grad / Masters / Doc 15

63%

Researcher 5

21%

Professor / Associate Prof. 4

17%

Readers' Discipline

Tooltip

Physics and Astronomy 21

81%

Chemistry 2

8%

Materials Science 2

8%

Engineering 1

4%

Save time finding and organizing research with Mendeley

Sign up for free
0