Heralded magnetism in non-Hermitian atomic systems

Abstract

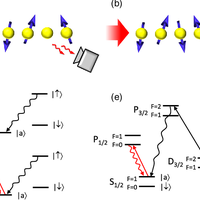
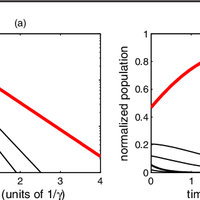
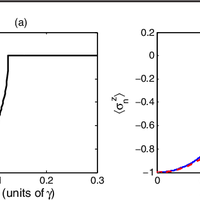
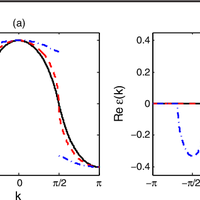
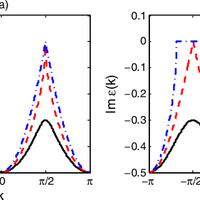
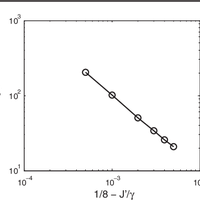
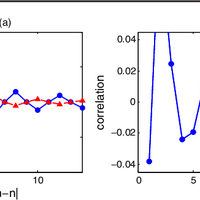
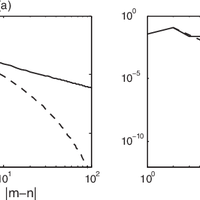
Quantum phase transitions are usually studied in terms of Hermitian Hamiltonians. However, cold-atom experiments are intrinsically non-Hermitian because of spontaneous decay. Here, we show that non- Hermitian systems exhibit quantum phase transitions that are beyond the paradigm of Hermitian physics. We consider the non-Hermitian XY model, which can be implemented using three-level atoms with spontaneous decay. We exactly solve the model in one dimension and show that there is a quantum phase transition from short-range order to quasi-long-range order despite the absence of a continuous symmetry in the Hamiltonian. The ordered phase has a frustrated spin pattern. The critical exponent ν can be 1 or 1=2. Our results can be seen experimentally with trapped ions, cavity QED, and atoms in optical lattices.