Computational modeling reveals that a combination of chemotaxis and differential adhesion leads to robust cell sorting during tissue patterning

Abstract

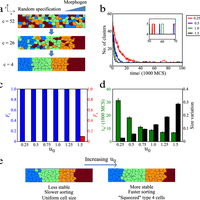
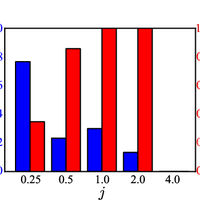
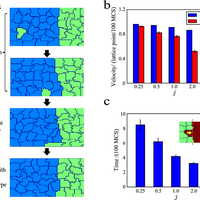
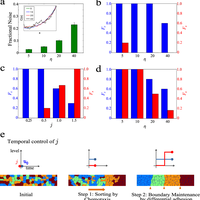
Robust tissue patterning is crucial to many processes during development. The "French Flag" model of patterning, whereby naïve cells in a gradient of diffusible morphogen signal adopt different fates due to exposure to different amounts of morphogen concentration, has been the most widely proposed model for tissue patterning. However, recently, using timelapse experiments, cell sorting has been found to be an alternative model for tissue patterning in the zebrafish neural tube. But it remains unclear what the sorting mechanism is. In this article, we used computational modeling to show that two mechanisms, chemotaxis and differential adhesion, are needed for robust cell sorting. We assessed the performance of each of the two mechanisms by quantifying the fraction of correct sorting, the fraction of stable clusters formed after correct sorting, the time needed to achieve correct sorting, and the size variations of the cells having different fates. We found that chemotaxis and differential adhesion confer different advantages to the sorting process. Chemotaxis leads to high fraction of correct sorting as individual cells will either migrate towards or away from the source depending on its cell type. However after the cells have sorted correctly, there is no interaction among cells of the same type to stabilize the sorted boundaries, leading to cell clusters that are unstable. On the other hand, differential adhesion results in low fraction of correct clusters that are more stable. In the absence of morphogen gradient noise, a combination of both chemotaxis and differential adhesion yields cell sorting that is both accurate and robust. However, in the presence of gradient noise, the simple combination of chemotaxis and differential adhesion is insufficient for cell sorting; instead, chemotaxis coupled with delayed differential adhesion is required to yield optimal sorting.