Monte Carlo simulations of microtubule arrays: The critical roles of rescue transitions, the cell boundary, and tubulin concentration in shaping microtubule distributions

Abstract

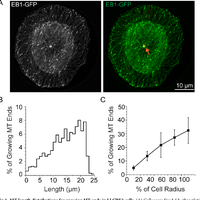
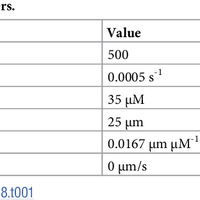
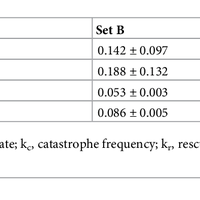
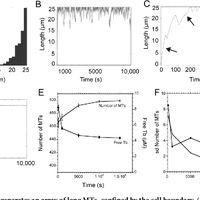
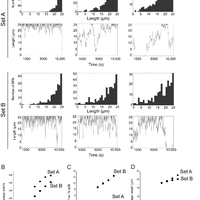
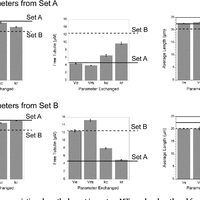
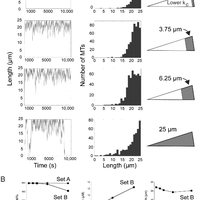
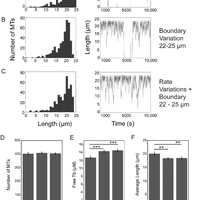
Microtubules are dynamic polymers required for a number of processes, including chromosome movement in mitosis. While regulators of microtubule dynamics have been well characterized, we lack a convenient way to predict how the measured dynamic parameters shape the entire microtubule system within a cell, or how the system responds when specific parameters change in response to internal or external signals. Here we describe a Monte Carlo model to simulate an array of dynamic microtubules from parameters including the cell radius, total tubulin concentration, microtubule nucleation rate from the centrosome, and plus end dynamic instability. The algorithm also allows dynamic instability or position of the cell edge to vary during the simulation. Outputs from simulations include free tubulin concentration, average microtubule lengths, length distributions, and individual length changes over time. Using this platform and reported parameters measured in interphase LLCPK1 epithelial cells, we predict that sequestering ~ 15–20% of total tubulin results in fewer microtubules, but promotes dynamic instability of those remaining. Simulations also predict that lowering nucleation rate will increase the stability and average length of the remaining microtubules. Allowing the position of the cell’s edge to vary over time changed the average length but not the number of microtubules and generated length distributions consistent with experimental measurements. Simulating the switch from interphase to prophase demonstrated that decreased rescue frequency at prophase is the critical factor needed to rapidly clear the cell of interphase microtubules prior to mitotic spindle assembly. Finally, consistent with several previous simulations, our results demonstrate that microtubule nucleation and dynamic instability in a confined space determines the partitioning of tubulin between monomer and polymer pools. The model and simulations will be useful for predicting changes to the entire microtubule array after modification to one or more parameters, including predicting the effects of tubulin-targeted chemotherapies.