Global motions of the nuclear pore complex: Insights from elastic network models

Abstract

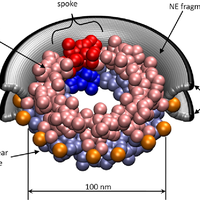
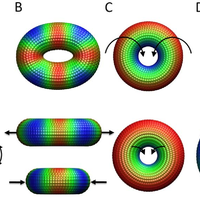
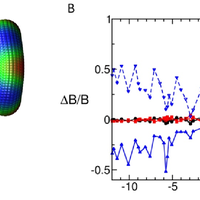
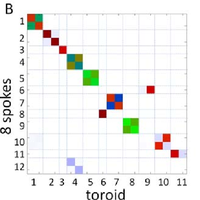
The nuclear pore complex (NPC) is the gate to the nucleus. Recent determination of the configuration of proteins in the yeast NPC at ,5 nm resolution permits us to study the NPC global dynamics using coarse-grained structural models. We investigate these large-scale motions by using an extended elastic network model (ENM) formalism applied to several coarse-grained representations of the NPC. Two types of collective motions (global modes) are predicted by the ENMs to be intrinsically favored by the NPC architecture: global bending and extension/contraction from circular to elliptical shapes. These motions are shown to be robust against tested variations in the representation of the NPC, and are largely captured by a simple model of a toroid with axially varying mass density. We demonstrate that spoke multiplicity significantly affects the accessible number of symmetric low-energy modes of motion; the NPC-like toroidal structures composed of 8 spokes have access to highly cooperative symmetric motions that are inaccessible to toroids composed of 7 or 9 spokes. The analysis reveals modes of motion that may facilitate macromolecular transport through the NPC, consistent with previous experimental observations. © 2009 Lezon et al.