Skip to main content
Journal ArticleOPEN ACCESS

An asymptotic expansion for a ratio of products of gamma functions

  • Bühring W
International Journal of Mathematics and Mathematical Sciences (2000) 24(8) 505-510
DOI: 10.1155/s0161171200010310
N/ACitations
Citations of this article
16Readers
Mendeley users who have this article in their library.

This article is free to access.

Abstract

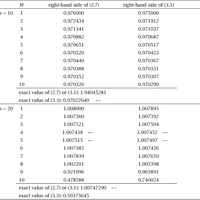
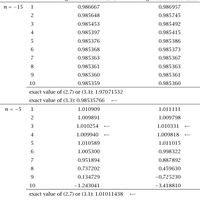
An asymptotic expansion of a ratio of products of gamma functions is derived. It generalizes a formula which was stated by Dingle, first proved by Paris, and recently reconsidered by Olver

Figures

  • Table 3.1. Values of the right-hand sides of (2.7) and (3.1) for the parameters a=−11.7, b =−11.2, c =−11.4.
  • Table 3.2. Values of the right-hand sides of (2.7) or (3.1) for the parameters a= 11.7, b = 11.2, c = 11.4.

Register to see more suggestions

Mendeley helps you to discover research relevant for your work.

Already have an account?

Cite

CITATION STYLE

APA

Bühring, W. (2000). An asymptotic expansion for a ratio of products of gamma functions. International Journal of Mathematics and Mathematical Sciences, 24(8), 505–510. https://doi.org/10.1155/s0161171200010310

Readers over time

‘10‘11‘12‘13‘15‘16‘17‘18‘20‘2201234

Readers' Seniority

Tooltip

Professor / Associate Prof. 8

57%

PhD / Post grad / Masters / Doc 4

29%

Researcher 2

14%

Readers' Discipline

Tooltip

Mathematics 10

67%

Physics and Astronomy 3

20%

Energy 1

7%

Agricultural and Biological Sciences 1

7%

Save time finding and organizing research with Mendeley

Sign up for free
0