An interactive channel model of the basal ganglia: Bifurcation analysis under healthy and Parkinsonian conditions

Abstract

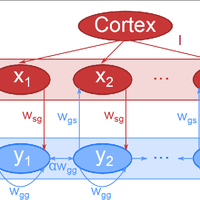
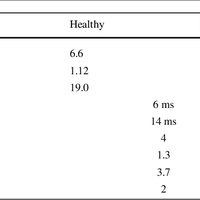
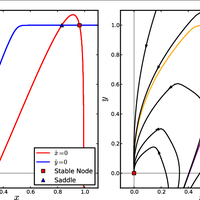
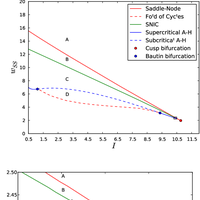
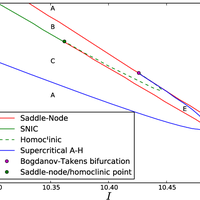
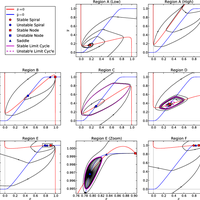
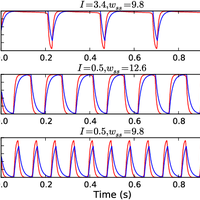
Oscillations in the basal ganglia are an active area of research and have been shown to relate to the hypokinetic motor symptoms of Parkinson's disease. We study oscillations in a multi-channel mean field model, where each channel consists of an interconnected pair of subthalamic nucleus and globus pallidus sub-populations. To study how the channels interact, we perform two-dimensional bifurcation analysis of a model of an individual channel, which reveals the critical boundaries in parameter space that separate different dynamical modes; these modes include steadystate, oscillatory, and bi-stable behaviour. Without self-excitation in the subthalamic nucleus a single channel cannot generate oscillations, yet there is little experimental evidence for such self-excitation. Our results show that the interactive channel model with coupling via pallidal sub-populations demonstrates robust oscillatory behaviour without subthalamic self-excitation, provided the coupling is sufficiently strong. We study the model under healthy and Parkinsonian conditions and demonstrate that it exhibits oscillations for a much wider range of parameters in the Parkinsonian case. In the discussion, we show how our results compare with experimental findings and discuss their possible physiological interpretation. For example, experiments have found that increased lateral coupling in the rat basal ganglia is correlated with oscillations under Parkinsonian conditions. © 2013 R. Merrison-Hort et al.