Abstract
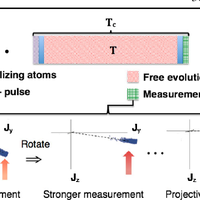
The ultimate stability of atomic clocks is limited by the quantum noise of the atoms. To reduce this noise it has been suggested to use entangled atomic ensembles with reduced atomic noise. Potentially this can push the stability all the way to the limit allowed by the Heisenberg uncertainty relation, which is denoted the Heisenberg limit. In practice, however, entangled states are often more prone to decoherence, which may prevent reaching this performance. Here we present an adaptive measurement protocol that in the presence of a realistic source of decoherence enables us to get near-Heisenberg-limited stability of atomic clocks using entangled atoms. The protocol may thus realize the full potential of entanglement for quantum metrology despite the detrimental influence of decoherence. © 2013 American Physical Society.
Figures
Register to see more suggestions
Mendeley helps you to discover research relevant for your work.
Cite
CITATION STYLE
Borregaard, J., & Sørensen, A. S. (2013). Near-heisenberg-limited atomic clocks in the presence of decoherence. Physical Review Letters, 111(9). https://doi.org/10.1103/PhysRevLett.111.090801

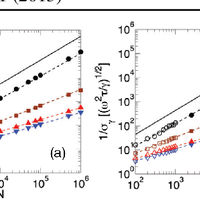
![FIG. 1 (color online). (a) The atomic state just before the measurement of Jz for (A) uncorrelated atoms, (B) moderately squeezed atoms, and (C) highly squeezed atoms. (b) Stability as a function of the Ramsey time ( T) for N ¼ 105. j, (.) is the conventional protocol of Ref. [5] for optimal squeezing (uncorrelated) atoms while d, (m) is the adaptive protocol for optimal squeezing (uncorrelated) atoms. The adaptive protocol allows for T 0:3 while the conventional protocol only allows for T 0:1 (see the Supplemental Material [32]).](https://s3-eu-west-1.amazonaws.com/com.mendeley.prod.article-extracted-content/images/c30c0278-d3e2-3a86-aa34-ea03765e48c9/thumbnail-f27f4437-4832-4ba2-a79b-8da9304f7458-0.png)