PoCos: Population Covering Locus Sets for Risk Assessment in Complex Diseases

Abstract

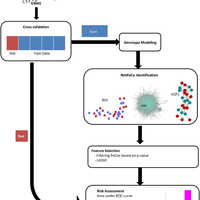
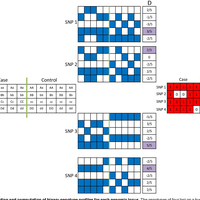
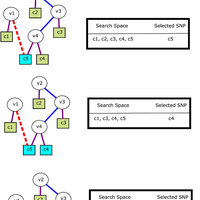
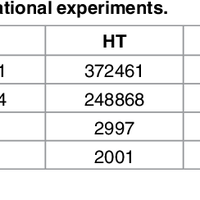
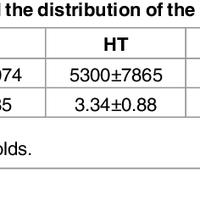
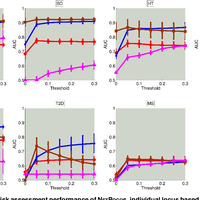
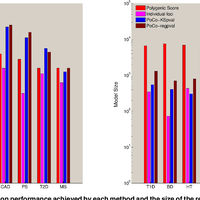
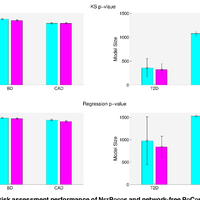
Susceptibility loci identified by GWAS generally account for a limited fraction of heritability. Predictive models based on identified loci also have modest success in risk assessment and therefore are of limited practical use. Many methods have been developed to overcome these limitations by incorporating prior biological knowledge. However, most of the information utilized by these methods is at the level of genes, limiting analyses to variants that are in or proximate to coding regions. We propose a new method that integrates protein protein interaction (PPI) as well as expression quantitative trait loci (eQTL) data to identify sets of functionally related loci that are collectively associated with a trait of interest. We call such sets of loci “population covering locus sets” (PoCos). The contributions of the proposed approach are three-fold: 1) We consider all possible genotype models for each locus, thereby enabling identification of combinatorial relationships between multiple loci. 2) We develop a framework for the integration of PPI and eQTL into a heterogenous network model, enabling efficient identification of functionally related variants that are associated with the disease. 3) We develop a novel method to integrate the genotypes of multiple loci in a PoCo into a representative genotype to be used in risk assessment. We test the proposed framework in the context of risk assessment for seven complex diseases, type 1 diabetes (T1D), type 2 diabetes (T2D), psoriasis (PS), bipolar disorder (BD), coronary artery disease (CAD), hypertension (HT), and multiple sclerosis (MS). Our results show that the proposed method significantly outperforms individual variant based risk assessment models as well as the state-of-the-art polygenic score. We also show that incorporation of eQTL data improves the performance of identified POCOs in risk assessment. We also assess the biological relevance of PoCos for three diseases that have similar biological mechanisms and identify novel candidate genes. The resulting software is publicly available at http://compbio.case.edu/pocos/.