Abstract
Many systems featuring nonlinearities and delay-free loops are of interest in digital audio, particularly in virtual analog and physical modeling applications. Many of these systems can be posed as systems of implicitly related ordinary differential equations. Provided each equation in the network is itself an explicit one, straightforward numerical solvers may be employed to compute the output of such systems without resorting to linearization or matrix inversions for every parameter change. This is a cheap and effective means for synthesizing delay-free, nonlinear systems without resorting to large lookup tables, iterative methods, or the insertion of fictitious delay and is therefor suitable for real-time applications. Several examples are shown to illustrate the efficacy of this approach.
Figures
Author supplied keywords
Register to see more suggestions
Mendeley helps you to discover research relevant for your work.
Cite
CITATION STYLE
Medine, D. (2016). Dynamical systems for audio Synthesis: Embracing nonlinearities and delay-free loops. Applied Sciences, 6(5). https://doi.org/10.3390/app6050134

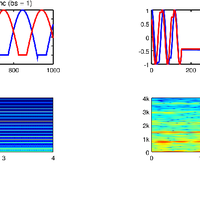
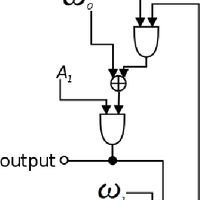
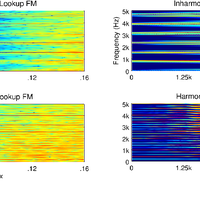
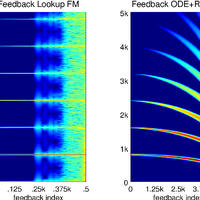
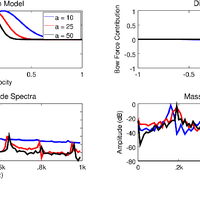
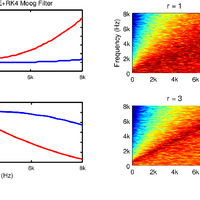
![Figure 7. The bowed oscillator model given here (solved with RK4) and that given in [21]. In both implementations, oscillator frequency f = 200, Fb = 500, vb = .2 and a = 100. (a) The system given in Equation (25) solved using RK4; (b) Using Newton-Raphson and Backward Euler to solve Equation (23).](https://s3-eu-west-1.amazonaws.com/com.mendeley.prod.article-extracted-content/images/e1f122a7-8ba7-312f-b4d2-d93653a56f7b/thumbnail-e407184c-b02c-4f6a-9c0c-3eaa09bbc990-5.png)