Abstract
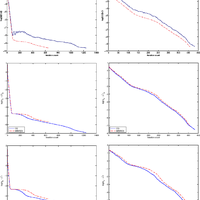
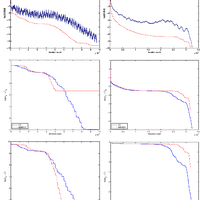
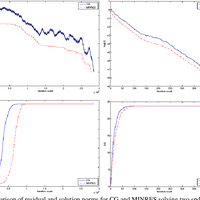
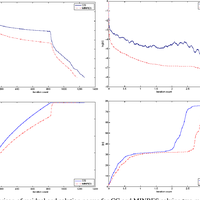
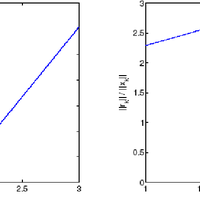
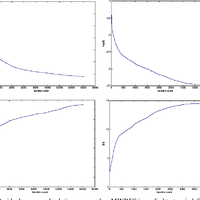
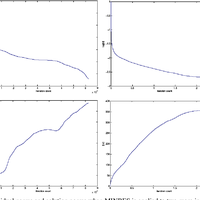
For iterative solution of symmetric systems the conjugate gradient method (CG) is commonly used when A is positive definite, while the minimum residual method (MINRES) is typically reserved for indefinite systems. We investigate the sequence of approximate solutions generated by each method and suggest that even if A is positive definite, MINRES may be preferable to CG if iterations are to be terminated early. In particular, we show for MINRES that the solution norms are monotonically increasing when A is positive definite (as was already known for CG), and the solution errors are monotonically decreasing. We also show that the backward errors for the MINRES iterates are monotonically decreasing.
Figures
Register to see more suggestions
Mendeley helps you to discover research relevant for your work.
Cite
CITATION STYLE
Chin-Lung Fong, D., & Saunders, M. (2012). CG Versus MINRES: An Empirical Comparison. Sultan Qaboos University Journal for Science [SQUJS], 16, 44. https://doi.org/10.24200/squjs.vol17iss1pp44-62